直線の平行や垂直, 平行や台形, 平行四辺形, ひし形などの概念について理解し,それらを弁別する力や作図する力を高めるとともに,これらを用いて図形の性質をとらえることができる。作図の小部屋 基本の作図 線分の垂直二等分線・外接円 角の二等分線・内接円 点から直線へ垂線をひく 線分の端点から垂線をたてる 点を通る平行線をひく 線分を5等分する「平行四辺形もかけるかな?」 ~図形を見ずに合同な形を作図する~ ☆本時のねらい:平行四辺形は,形と大きさが決まる要素が三角形の場合と違うこ とを理解し,合同な平行四辺形をかくことができ

最新 平行 四辺 形 書き方 コンパス
平行四辺形作図 指導案
平行四辺形作図 指導案-平行四辺形に内接する楕円の作図 岩渕清行 To lnscribe a Ellipse in a Parallelogram Seik5 1WABUTI Abstract This is a method of no plincipal axes and no con,ugate diameter YOu may draⅥr any inscribed e ipse of parallelogran directry by this method 1。 まえがき 平行四辺形の作図方法について見ていこう まずは、三角定規をこのような形にセットします。 そして、定規を上にスライドさせ平行な線を引きます。 もう一方の線に対しても、同様に平行線を引きます。 すると、2つの平行線が交わるところ ここが




小学4年 023 算数 平行四辺形の書き方 Youtube
平行四辺形の作図方法 を考えることができ る。 垂直や平行な 直線をかくこと ができる。 四角形を弁別 して,平行四辺 形を作図するこ とができる。 直線の交わり方につ いて,垂直や平行の関 係にあることの意味を 理解する。 台形,平行四辺形,技 台形,平行四辺形をかくこ とができる。 9 / 15 平行四辺形のひみつを見つけよう。 ・ 2枚の平行四辺形の紙を使って, 平行四辺形の特徴を調べる。 ・ 平行四辺形の性質をまとめる。 ・具体物を用いた 活動 ・説明する活動 考 辺の並び方,辺の長さ,角すると、傾斜がついて平行四辺形になります 上記の方法以外に「メニュー/オブジェクト/変形」の「傾斜」が使えます 水平に数値を入力して適用すると傾斜がつきます 今回はこれでおしまい、また
れた平行四辺形を渡し,かい た平行四辺形が合同か確かめ させる。 ・実物投影機でかき方を確認す る。 ・どの辺や角を測って作図した のかを意識させるように教師 が色分けや順番を考え黒板に 提示する。 ・辺adと辺cdのかき方はいろ いろあるが共通して行四辺形を作図す 平行線のかき方を確認する。 うとしている。 る。 〈イ4,ア1・3〉 5 (5)それぞれの方法で ・ それぞれの作図の方法が, ・ 作図の方法と平行四辺 本時 平行四辺形の作図が 平行四辺形の定義や性質と結 形の定義や性質が結び付また、平行四辺形、ひし形、台形を弁別し性質を見出すだけでなく、既習 本時目標 垂直と平行の作図を基に、四角形を作図する活動を通して、長方形や正方形の性質を捉え直すとともに、図形を統合的
三角形と四角形(直角三角形・正方形・長方形・辺・頂点・直角等)の概念を理解し、形の弁別の練習や作図の問題を通して理解を深めることができます。 小学4年生の算数 台形・平行四辺形・ひし形・対角線 問題プリント平行四辺形の作図の仕方を考え,説明する。 (1時間) ひし形の特徴を調べ,ひし形の意味や性質について理解する。 (1時間) 平行四辺形やひし形の対角線の交わり方を調べ,その特徴を理解する。 (1時間) 四角形の対角線による合成と分解をもとに図3の平行四辺形では,児童が「高さ」を作図 し,測定した際に,その値が整数になるのは, 長辺を底辺とした場合に限られる。また,平行 四辺形の配置が,短辺を「底辺」とした場合に 「高さ」が作図しにくいことから,「底辺を延長




Emath講座 平行四辺形の作図 数樂管理人のブログ




中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく
ひし形を作図する 平行線の作図は、まったく別の手順も可能です。 作図の基本であるひし形は、向かいあう辺が平行になっています。 よって、上図のようなひし形を作図できれば、おのずと直線 \(l\) の平行線を得ることができます。 正方形の作図 例題図形を描く・小学生算数ドリルのページへようこそ 上記のボタンから図形を描く・小学生算数ドリル (PDFプリント)がダウンロードできます。 個人利用は無料です (家庭以外での配布は有料です)。 スマートフォンやタブレットなどからも印刷できるように右の図形は正方形だ。平行な辺が2組で,4つの角もみんな直角になっているよ。 C あとは全部,平行四辺形だ。だって,平行な辺が2組あるから。 4 ひし形の特徴と用語を知る。 T 前の学習で作った平行四辺形とまったく同じかな。 C ん?




中2数学 平行線と面積の作図問題がわかる4ステップ Qikeru 学びを楽しくわかりやすく



物理の力の範囲です 作図により合力を求めなさいという問題で Yahoo 知恵袋
A 6 平行四辺形の作図 コンパスを使った平行四辺形のかき方について,用いられている平行 四辺形の特徴を選ぶ A 6 正答率 521% 「図形の約束や性質に基づいて作図しよう」 ~作図の方法と図形の約束や性質を関連付ける~平行四辺形から これら、対角線をはさむ二つの平行四辺形を 除いて残る 二つの平行四辺形をいう。 (以下、定義の補足(命題1-43)(対角線をはさむ平行四辺形・補形)という。) 命題1-44作図線分,三角形,直線角と平行四辺形)②平行四辺形は、対角線で分けた2つの三角形が合 であるこ とや三角形の作図の仕方などを掲示したり確認したりするこ とで、三角形のかき方を使っていることに気付くことができ るようにする。 〈視点1〉確かな見通しをもたせるための手立て



平行四辺形abcdがある この平行四辺形を図1のように 頂点dにかさな Yahoo 知恵袋



1
(1) 上の例のように平行四辺形の対角線を作図する方法 (2) 次の図のように、 三角形で作図する 方法 の2つの方法があります.結果は同じですが,3個以上のベクトルの和を作図するなど,問題が複雑になると(2)の三角形の方が作図しやすいので,以下は三角平行四辺形・対角線 (平行四辺形と長斜方形とは同義) (平行四辺形の対角線は互いに他を2等分) (作図隣り合う2辺から平行四辺形) 平行四辺形において 対辺および対角は互いに等しく、 対角線はこれを2等分する。 平行四辺形とは平行四辺形2 1.基準となる稜線を2本選択します。 この選択する稜線で平行四辺形の角度が決定されます。 2.平行四辺形の辺の長さを指定します。 数値の入力にはダイナミック入力が使用できます。 通常はアクティブな作業平面上に作図されますが




四角形と三角形の面積




小学4年 023 算数 平行四辺形の書き方 Youtube
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)た平行四辺形の作図をする。 <教科書p80、81> 平行四辺形を敷き詰めて、図形の性質を調べる。 <教科書p、> ひし形の定義や性質を理解し、作図する。 <教科書 84、85> 評価規準の例 いる。 ・「台形」「平行四辺形」の用語や定義を理解して第1巻命題44 三角形に等しい平行四辺形の作図 角と線分を与えられた場合 Stoixeia ストイケイア



図形に強くなる 正確な作図 2 中学受験ブログ
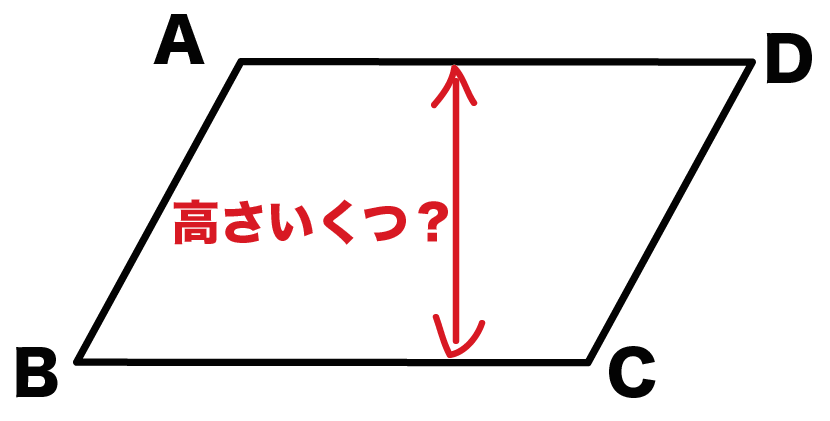



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく
平成23年度 中学校 数学a (7) 三角形の合同条件・平行四辺形に成るための根拠となる事柄 (pdf:142kb) 2年 平成21年度 中学校 数学a (7) 三角形の合同条件・図形の性質を記号で表すこと (pdf:152kb) 2年折り紙で作った平行四辺形を利用し て点対称の意味や性質を理解する。 出身小学校を含む校章や都道府県の マークから点対称な図形を探す。 島根県 兵庫県 折り紙でつくった二等辺三角形、台 形、平行四辺形、長方形、ひし形や★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料



Http Www Education Fukaya Saitama Jp Index Php Action Multidatabase Action Main Filedownload Download Flag 1 Upload Id 9423 Metadata Id 99
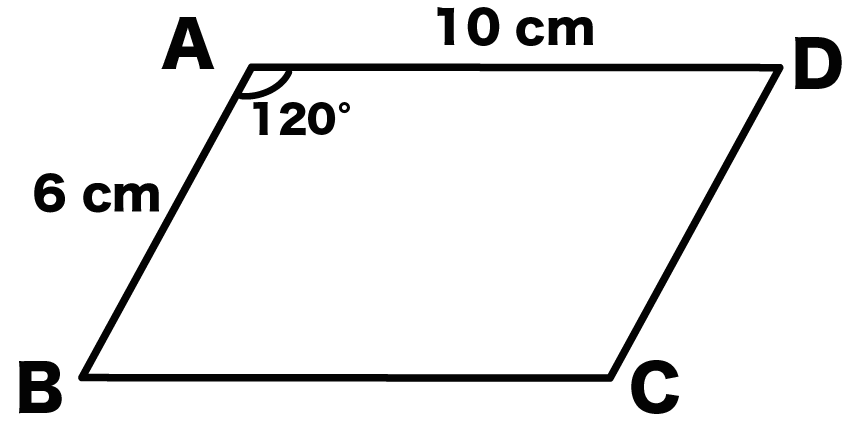



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
解説円の作図なので、円の中心と、半径を定めることが目標です。 完成図をラフスケッチして、図形的性質を探りましょう。 「接している」ということは、円の中心と接点を結ぶ半径は、接線と垂直です。 2乗に比例・平行四辺形の面積平行四辺形の定義や性質を基にして,方眼紙上の平行四辺形の底辺の長さ が5であることから,向かい合う平行な辺の長さが5と分かり,頂点が4で あると判断する。 誤答例1 1 または 5 向かい合う辺が平行であることについて誤って理解している。・垂直、平行の意味、性質、作図 ・垂直、平行を使った長方形の作図 ・台形、平行四辺形、ひし形の意味、性質、作図 ・四角形の対角線の考察 ・平行四辺形、台形を敷き詰めた図をかく活動 小学生・中学生が勉強するならスクールtv。全国の学校の教科書に対応した動画で学習できます。



Q Tbn And9gcsdxsdxc0jzbc5ziuqztfqvmad Gcke28kwbjendz478zsobswq Usqp Cau




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブラの作図機能を使って考えてみよう。 ジオジェブラは正確なので、図に頼らないで、なぜそのことが言えるのかをというわけで、平行四辺形を作図する手順について紹介していきます。 まずは、直線 上の好きなところにコンパスの針を置きます。 その点から点Aまでの距離を半径とする円をかきます。 すると、このように同じ長さの辺を作ることができますね。 次に長方形や平行四辺 形を対角線で分割し てできる,2 つの三角 形は合同であること を知り,これらを使っ ていろいろな四角形 る。 それぞれの四角形 の定義や性質の理解 を深め,平行四辺形・ 台形・ひし形をかくこ とができる。




4 Abcd Abcdbc Descubre Como Resolverlo En Qanda



Science 超簡単 力の合成と力の分解の基礎 働きアリ
平行四辺形を利用 もう一度、同じ問題を考えます。 点 F が作図できたとして、四角形 ACFD がどのようになっているかをよく見てみましょう。 線分 AD, CF は同じ長さです。 また、平行移動をしても移動前後で形や大きさは変わらないので、 $\mathrm{ AC=DF }$ です。



1



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




台形 平行四辺形 Youtube



Http Www Edu City Yokohama Lg Jp School Jhs Sakaigi Index Cfm 1 02 C Html 02 0508 Pdf




力の合力についてです 合力のヒントの点線に合わせて平行四辺形を作図するのですか Clear




力の合力についてです 合力のヒントの点線に合わせて平行四辺形を作図するのですか Clear




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形




動画で学習 3 台形と平行四辺形 算数
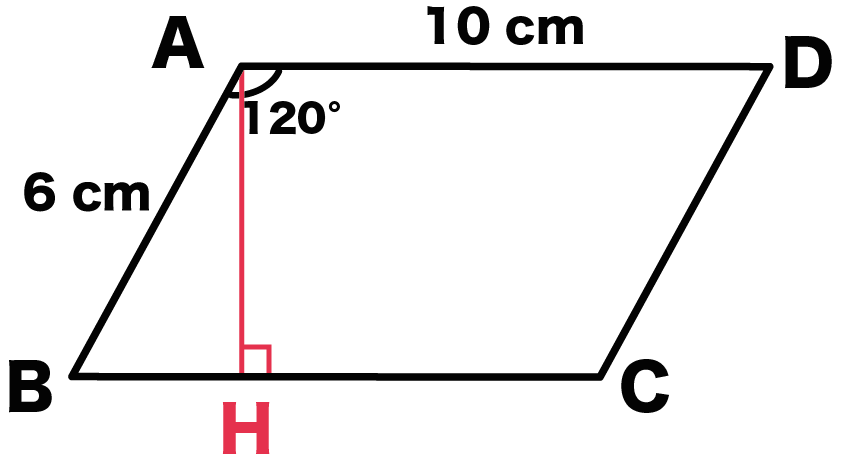



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




至急 1問でもいいので教えて下さい よろしくお願いします Clear




第1巻命題44 三角形に等しい平行四辺形の作図 角と線分を与えられた場合 Stoixeia ストイケイア




合力の作図 三角定規を使ったやり方は 中学理科の問題を解説 中学数学 理科の学習まとめサイト




標準 平行移動に関する作図 なかけんの数学ノート



合同な図形を作図しよう 5年 高岡市立下関小学校




最新 平行 四辺 形 書き方 コンパス
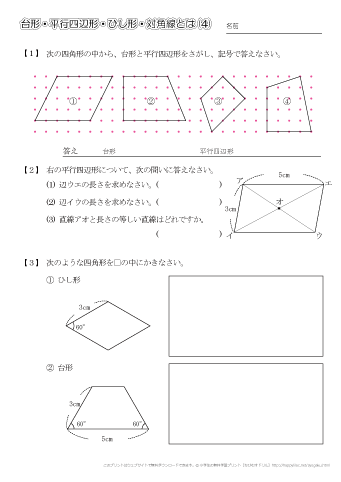



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生
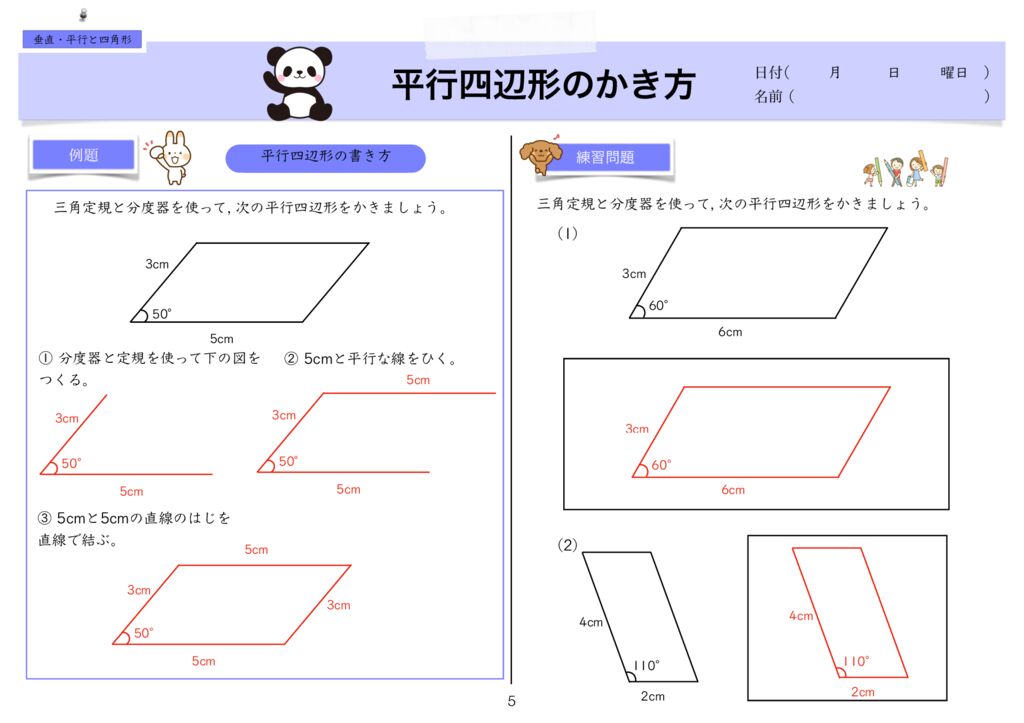



世界一分かりやすい算数 小4 垂直 平行と四角形
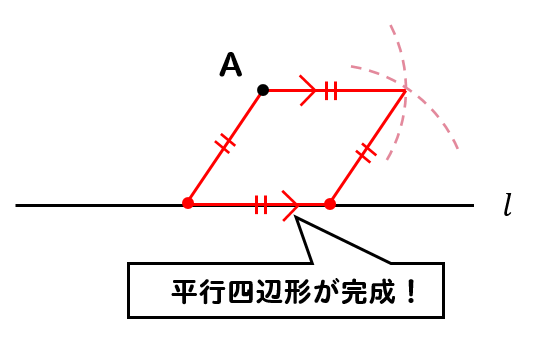



数学a作図 コンパスを使って平行線を作図する方法とは 数スタ
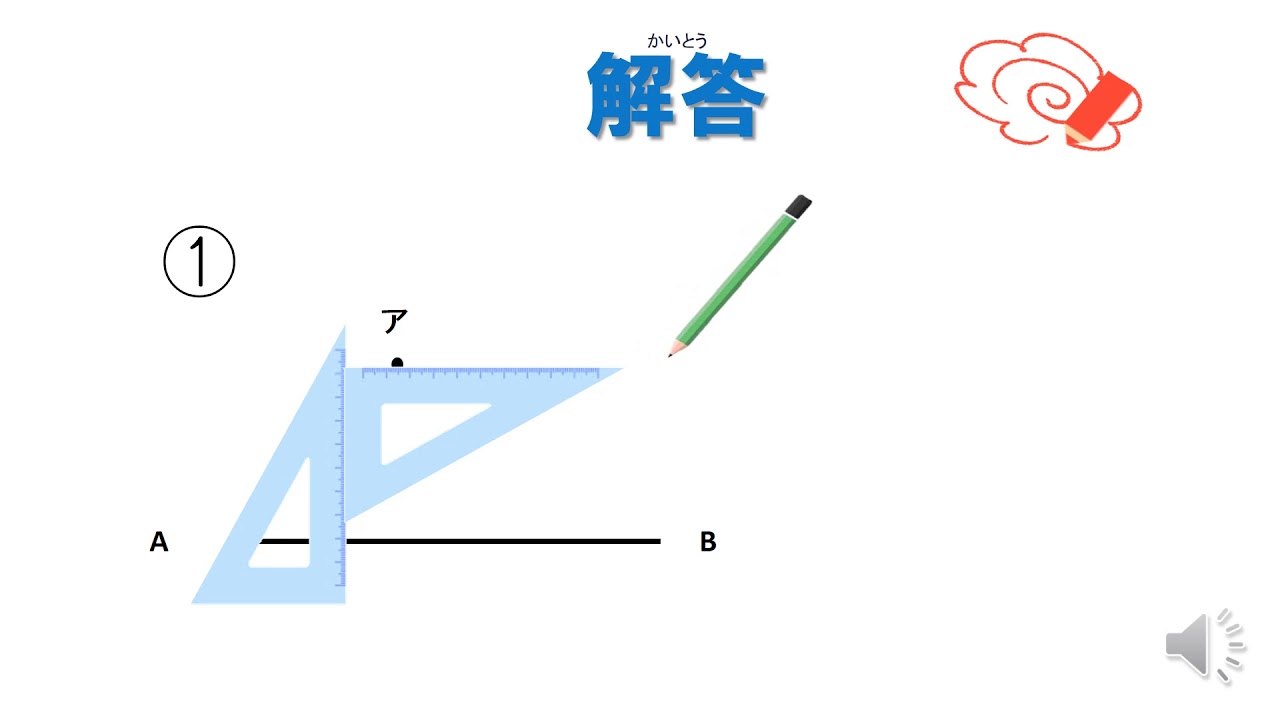



小3 平行線の書き方 三角定規 日本語版 Youtube




ベクトルの加法 怜悧玲瓏 高校数学を天空から俯瞰する



平行四辺形について知ろう 苦手な数学を簡単に




小4の息子 平行四辺形と台形の作図に苦戦 かずさんパパの親ばかブログ



最新 三角定規 平行 四辺 形 書き方



ベクトルの和



2



物理基礎です 平行四辺形の法則による作図法を用いて合力を作図せ Yahoo 知恵袋
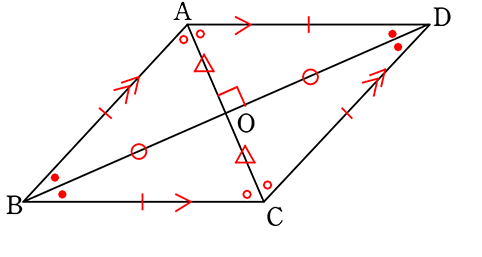



中学数学 平面図形



Http Www Hiroshima C Ed Jp Pdf Research Chouken R01 Zenki Zen05 Pdf



雑学のソムリエ 円に内接する




小4算数 垂直 平行と四角形 平行四辺形 ひし形の作図 Youtube




垂直二等分線 の作図方法 コンパス 定規 数学fun



対角線で参観 教育考現学
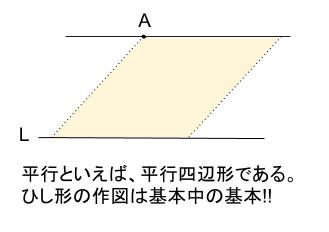



中学数学 作図 平行線 正方形 中学数学の無料オンライン学習サイトchu Su




平行四辺形で知っておくべきこと 苦手な数学を簡単に



平行四辺形と面積 2 ネット塾
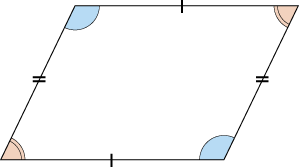



平行四辺形の性質 5年生 算数の広場




平行四辺形の簡単な書き方 超数学館match 数学に特化した徹底個別指導塾 高崎 前橋
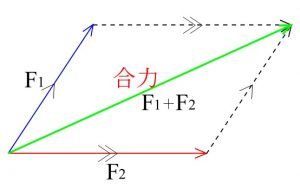



力の合成と分解とは 成分の作図は平行四辺形が基本
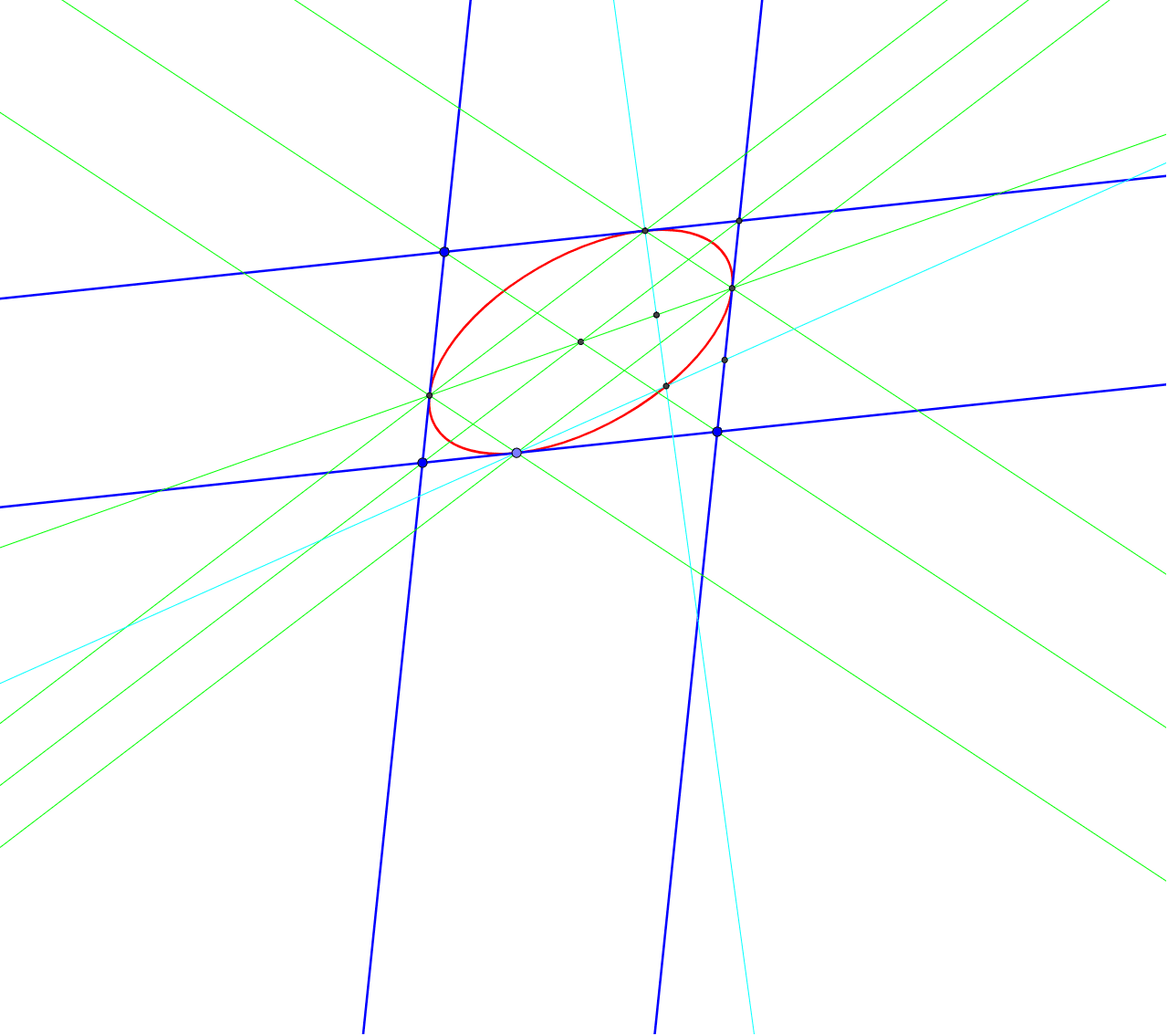



平行四辺形に内接する楕円 Geogebra



Http Www Saga Ed Jp Kenkyu Kenkyu Chousa H24 04 chu Suugaku Documents H24 Heimenzukei Worksheet 004 Pdf




平行四辺形の作図 方眼紙 スクールプレゼンター教材共有サイト スクプレ道場
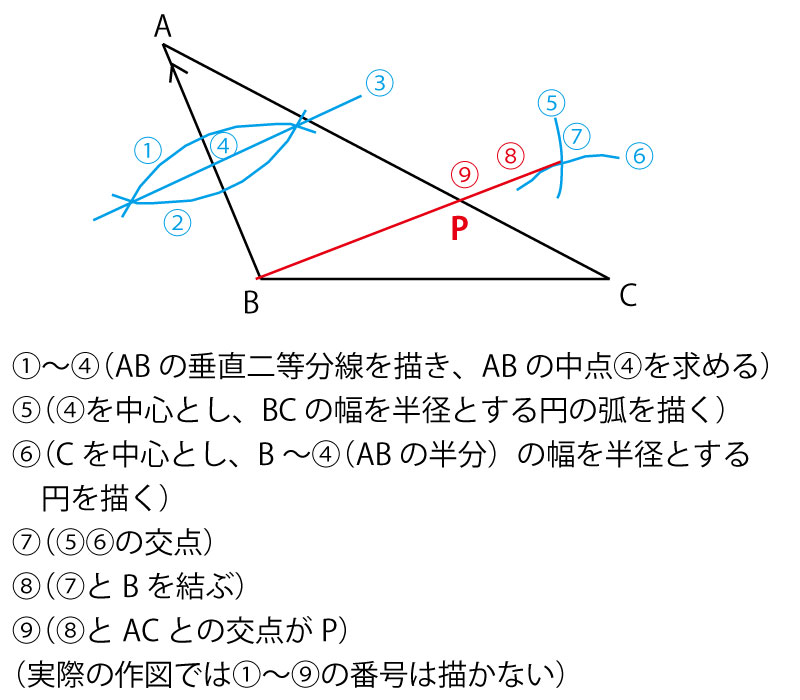



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




平行四辺形とひし形 19千葉県立 数学カフェjr
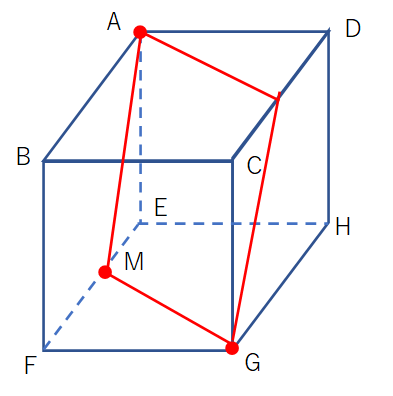



立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ
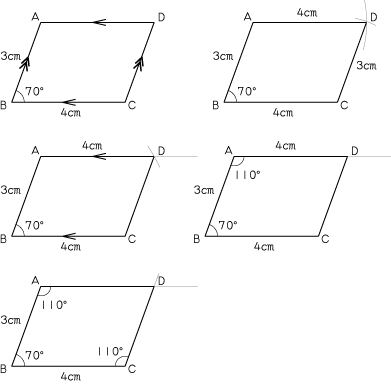



作図の足あと 算数の広場



コンパスと定規を使った正方形 正四角形 の描き方 図形の描き方013a 夏貸文庫
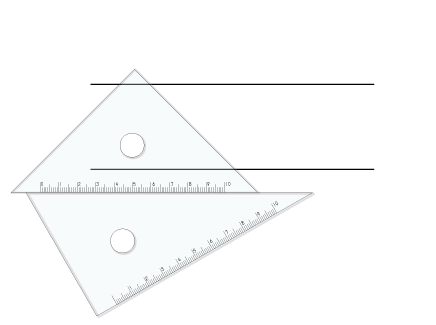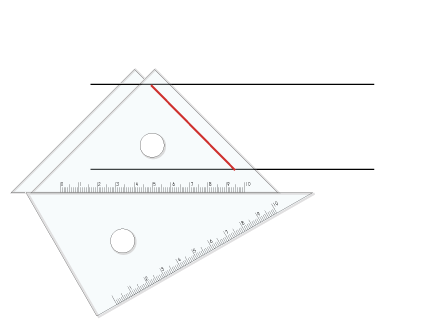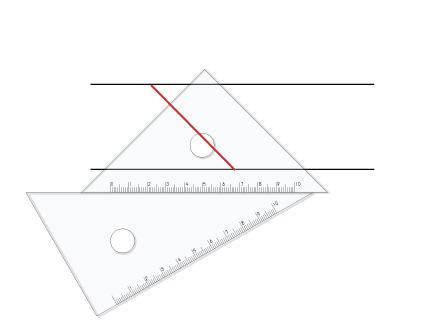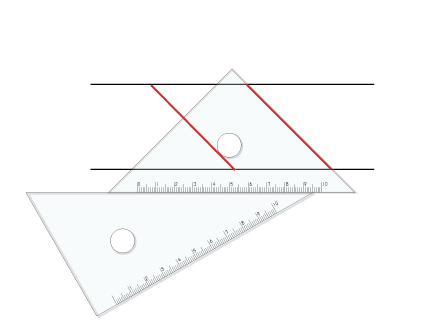



平行四辺形をかく 5年生 算数の広場
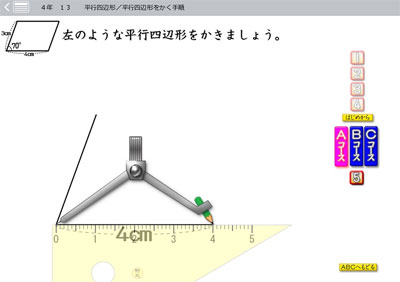



奥田先生が4年の 平行四辺形の作図 のソフトを さくら社



中1の図形なんですが平行四辺形abcd作図しなさいとあるんですが わからない Yahoo 知恵袋




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



2




第1巻命題44 三角形に等しい平行四辺形の作図 角と線分を与えられた場合 Stoixeia ストイケイア



1
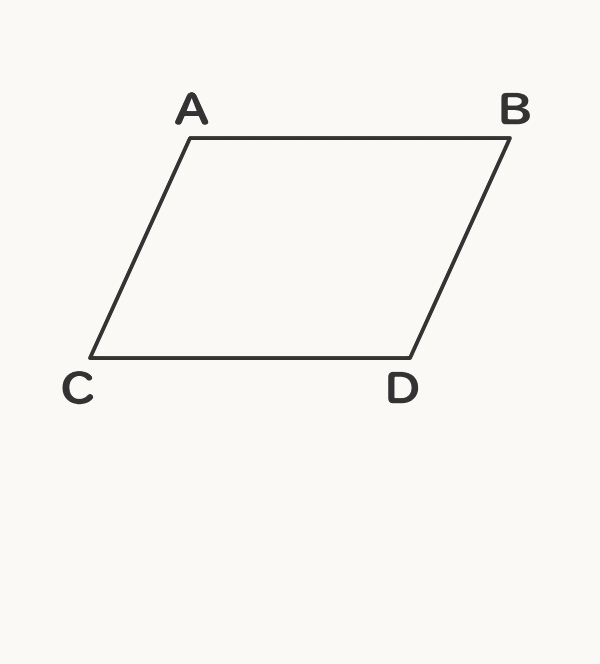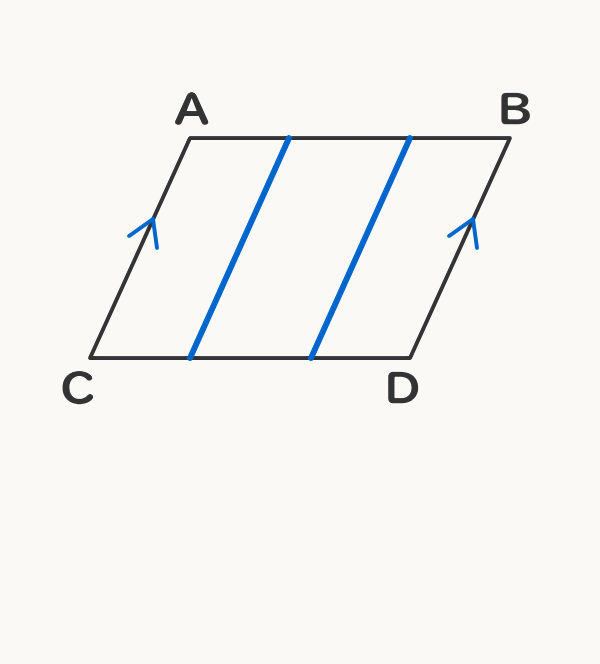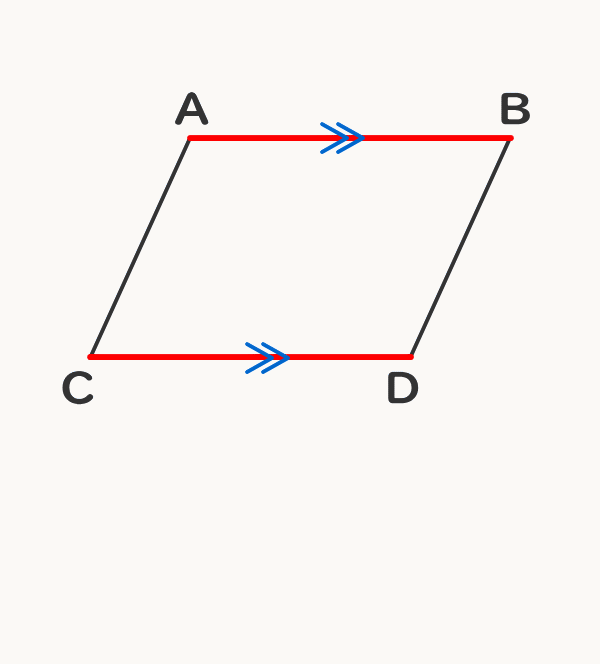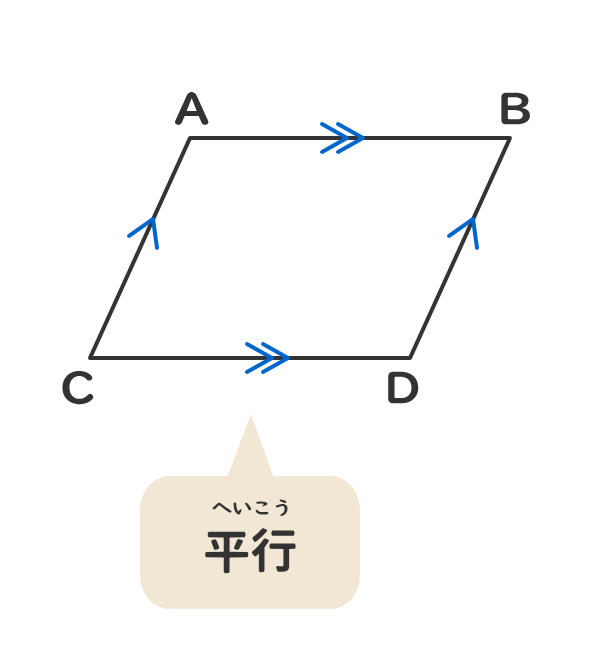



平行四辺形の仲間を知ろう 電験3種web




40個答えなくてはいけないようで 1人では出来ませんでした Clear
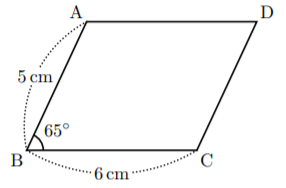



Emath講座 平行四辺形の作図 数樂管理人のブログ




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
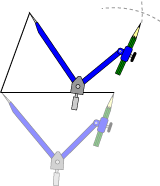



平行四辺形の作図 5年生 算数の広場




平行四辺形の仲間を知ろう 電験3種web
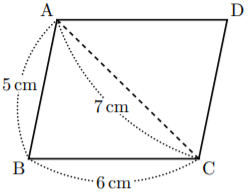



Emath講座 平行四辺形の作図 数樂管理人のブログ



中2数学 図形と合同5 平行線と面積 問題見本 プリント




平行四辺形の辺や角を求める Youtube




2力のつり合い 力の合成と分解 無料で使える中学学習プリント
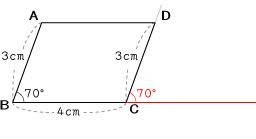



平行四辺形の作図 5年生 その4 算数の広場




ぬるいパースが描けるようになりたい 作図 2次元 作図してみる




力の平行四辺形 Wikiwand



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M13 Pdf



Www Pref Okayama Jp Uploaded Life Misc Pdf



中3です 分力の作図の問題で平行四辺形を書くタイプの問題に疑問があります Yahoo 知恵袋




数学の世界をのぞいてみよう 第51回 平行四辺形の作図 Segブログ 科学的教育グループseg



数学教育 幾何 図形 的見方 平行四辺形
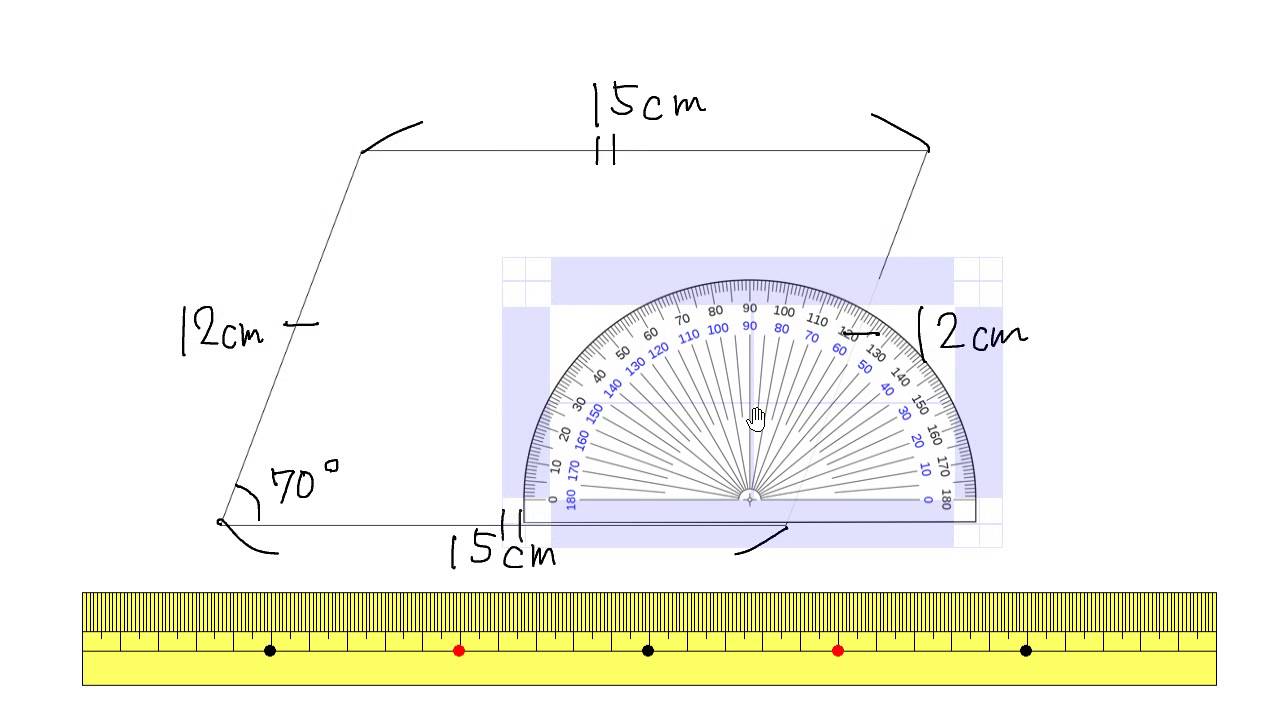



平行四辺形のきまり Youtube




作図の方法 教えてください Clear
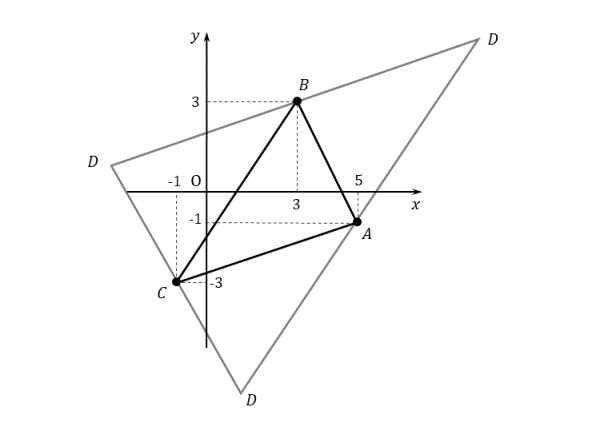



図形と方程式 平行四辺形の頂点の座標について 日々是鍛錬 ひびこれたんれん
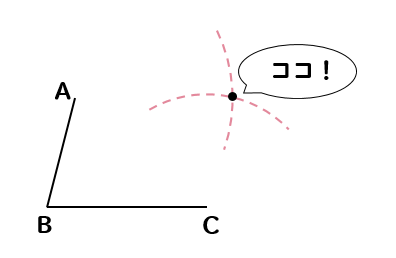



平行四辺形の書き方 コンパスを使って作図する方法は 数スタ



四角形 ひし形 平行四辺形 台形 の書き方 作図 まとめ 受験辞典



合同な図形を作図しよう 5年 高岡市立下関小学校
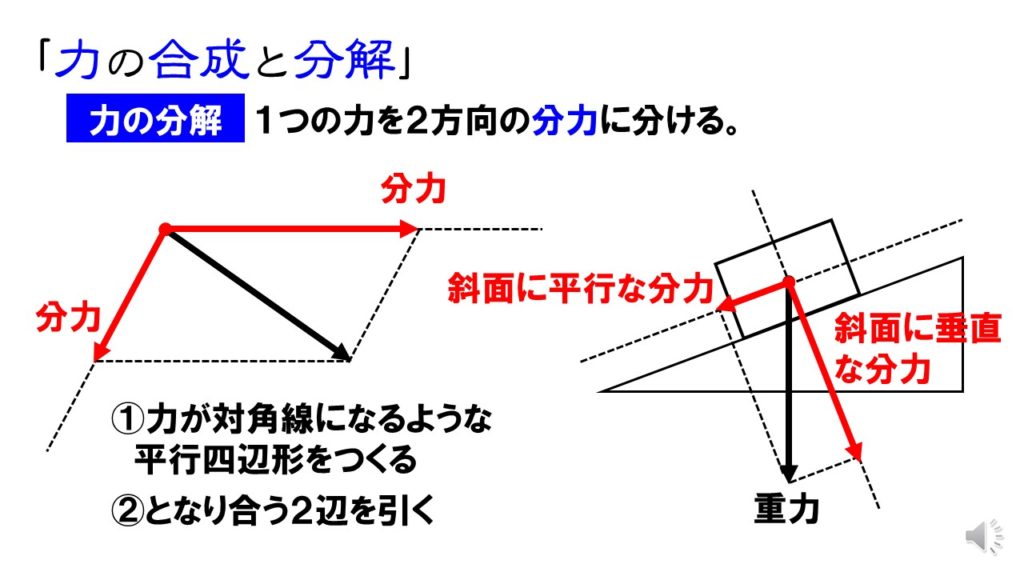



中3理科 力の合成と分解 合力や分力の作図 Pikuu



力の合成と分解の作図方法が教科書やネットをみても 三角定規で Yahoo 知恵袋
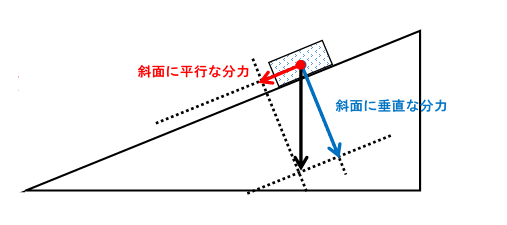



中3物理 力の合成 分解 中学理科 ポイントまとめと整理



Www Nier Go Jp Jugyourei H26 Data Pmath 02 Pdf
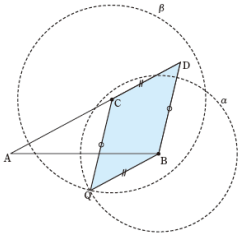



平行線の作図 内分点 外分点の作図について 数学 苦手解決q A 進研ゼミ高校講座
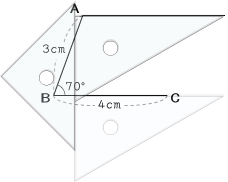



平行四辺形の作図 5年生 その3 算数の広場




Abcdbceadf Aecf Efef Adb Lihat Cara Penyelesaian Di Qanda
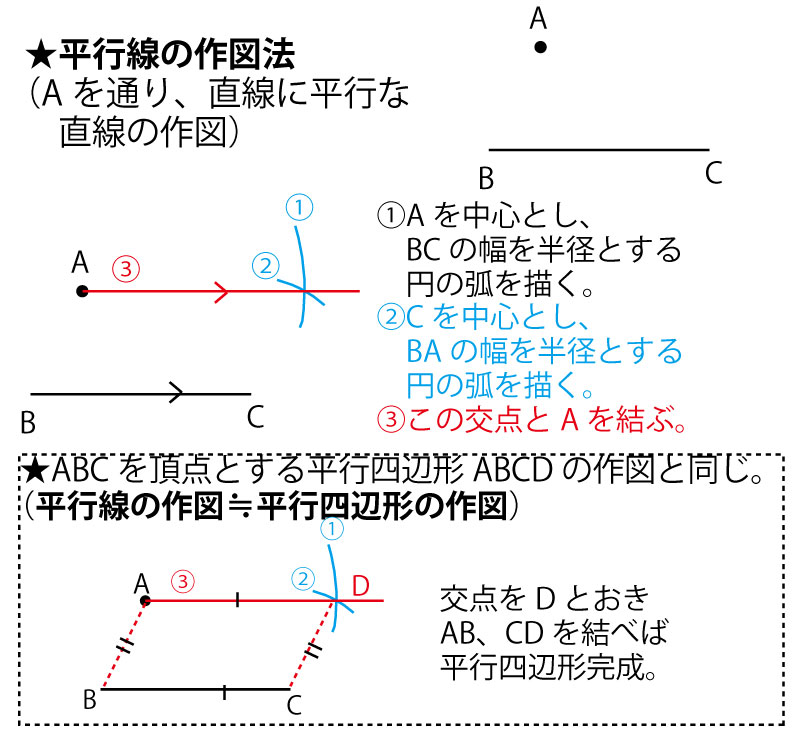



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



Www Pref Saitama Lg Jp Documents P47 48 Pdf




つな引きで勝つ引き方から考える 力の合成 と 合力の作図 理科の授業をふりかえる
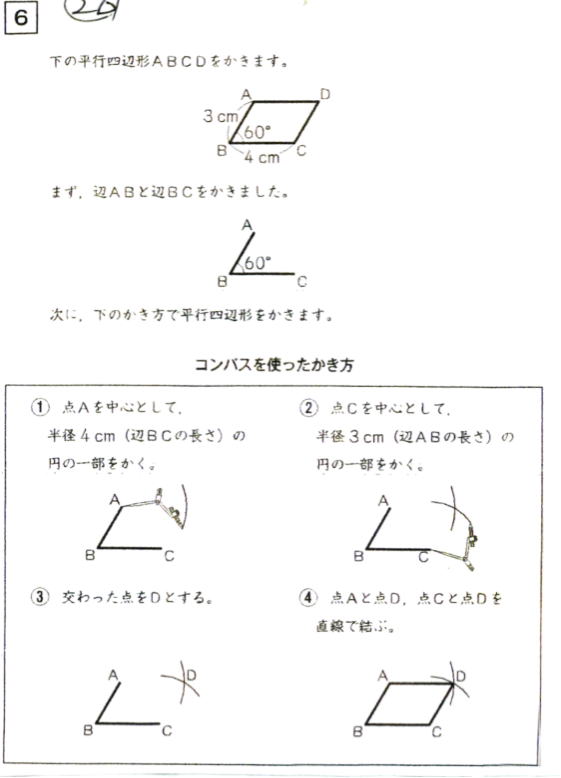



4年算数 垂直 平行と四角形 3 教え方のポイント



0 件のコメント:
コメントを投稿