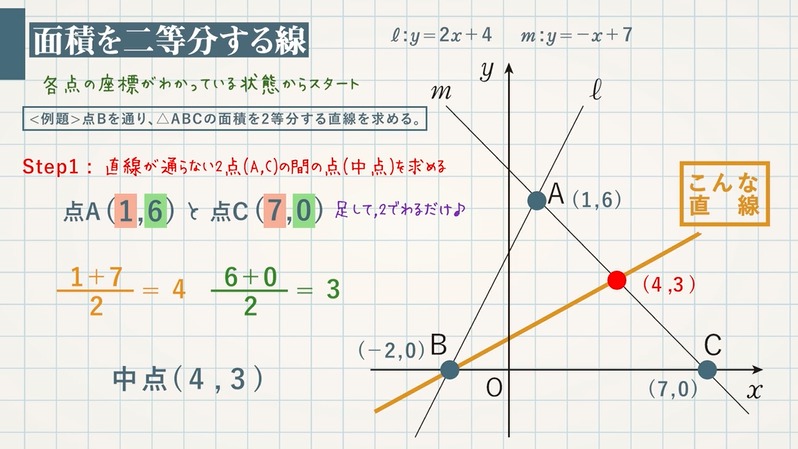
１次関数のグラフの応用 面積を二等分する線 面積が等しくなる点 教遊者
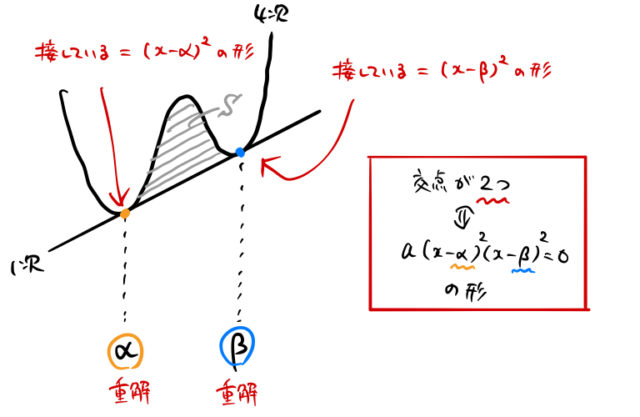
定番の1/6公式である。2次関数 と1次関数 の場合を考える。係数は適当に としている（ ）。 図は下のようになる。交点の 座標を小さい方から とした。2次関数の公式と計算 2次関数の公式は です。定数a、b、cの値が決まればxに値を代入してyの値を計算できます。なおy＝0のとき、 です。未知数xを求める場合、解の方程式で計算すると便利です。
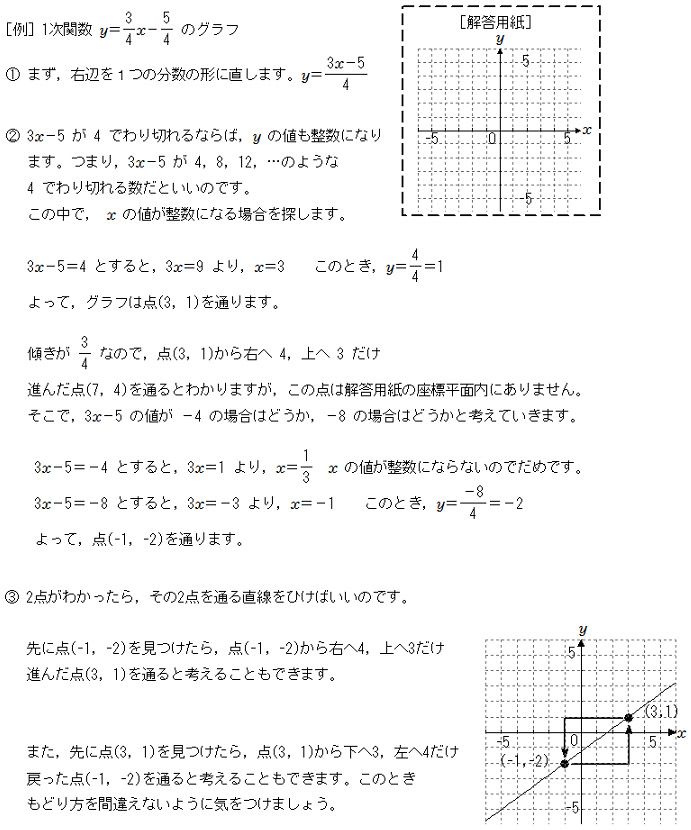
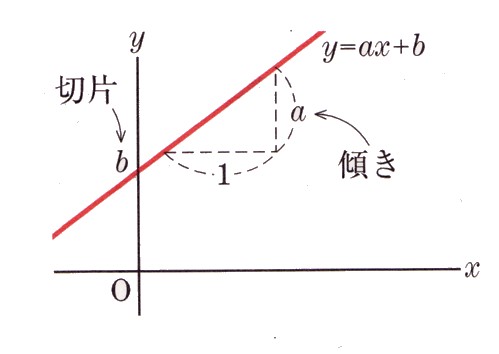
1次関数 2点を通る 公式
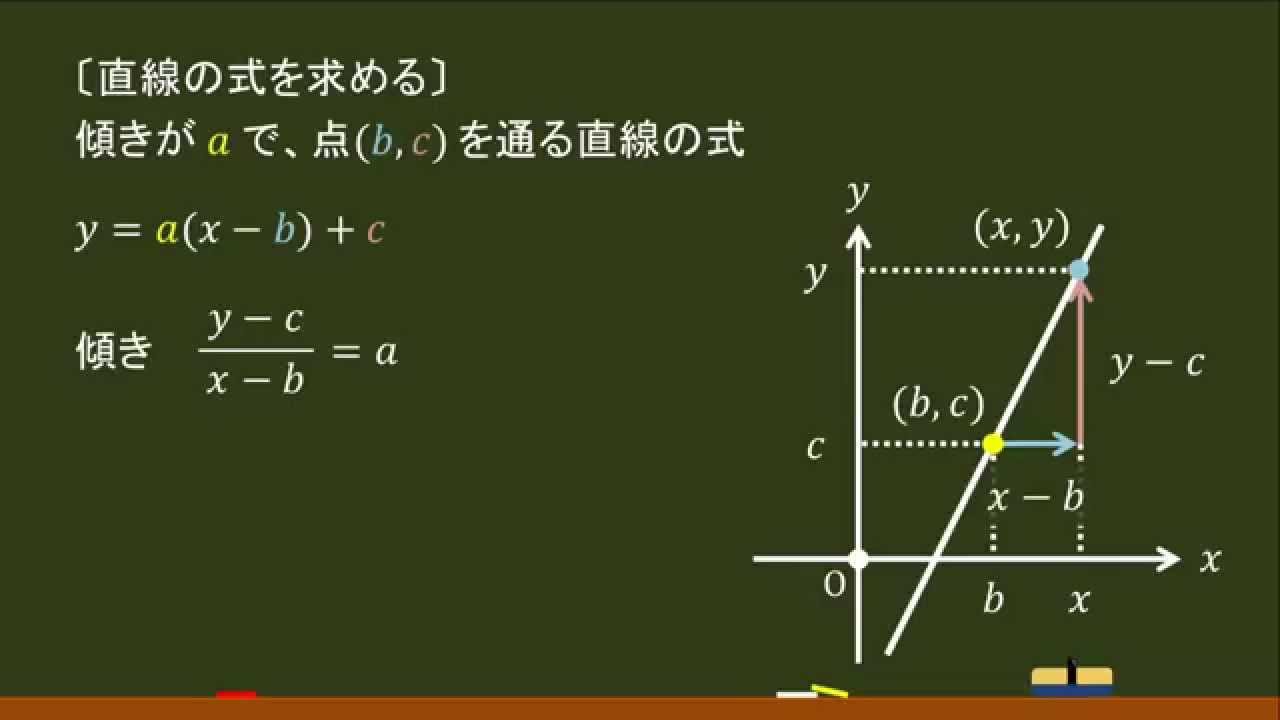
1次関数 2点を通る 公式-1次関数の公式 こんにちは。萃聚(すいじゅ)です。 公式 1次関数の直線のグラフにおいて、傾き $a$ で点 ($p$, $q$)を通る直線1 6 \dfrac{1}{6} 6 1 公式（ろくぶんのいち公式）を使うと，いろいろな面積の計算を素早くできます。 ぜひ覚えておきましょう。
高校数 関数 １次関数の方程式 定義域と値域から求める オンライン無料塾 ターンナップ Youtube
12 1 12 公式 (2次関数) 2次関数が絡んだ面積公式は 1/6公式 が有名で最重要ですが，2次関数と2接線で囲まれた面積もたまに入試で問われます． これを 1 12 1 12 公式と名付けると便利ですが，これ↦, = を一次関数と呼ぶ（見かけ上一次なだけで10 一次関数公式まとめ 101 Share this 102 関連
比例式 同様「× (かける)でつながっている公式 (〇＝ ・ ・ ・ )」のようなものは、すべて「1次関数」になれる可能性があるということですね！ →右辺の文字のうち、1つだけが文字 (変数)として残りこちらの記事で1から解説をしていまず。 一次関数が苦手だという方はまずはこちらの記事で復習しておいてください。 それでは、次の問題について解き方を順に確認していきましょう。 一次関 先ほどの公式を用いると、求める1次関数は\(y2=3(x1)\)と表せる。 これを整理して、\(y=3x1\)となる。 圧倒的楽勝感万歳！ なるほど。1次関数はここまで深められるのですね。 で
1次関数 2点を通る 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 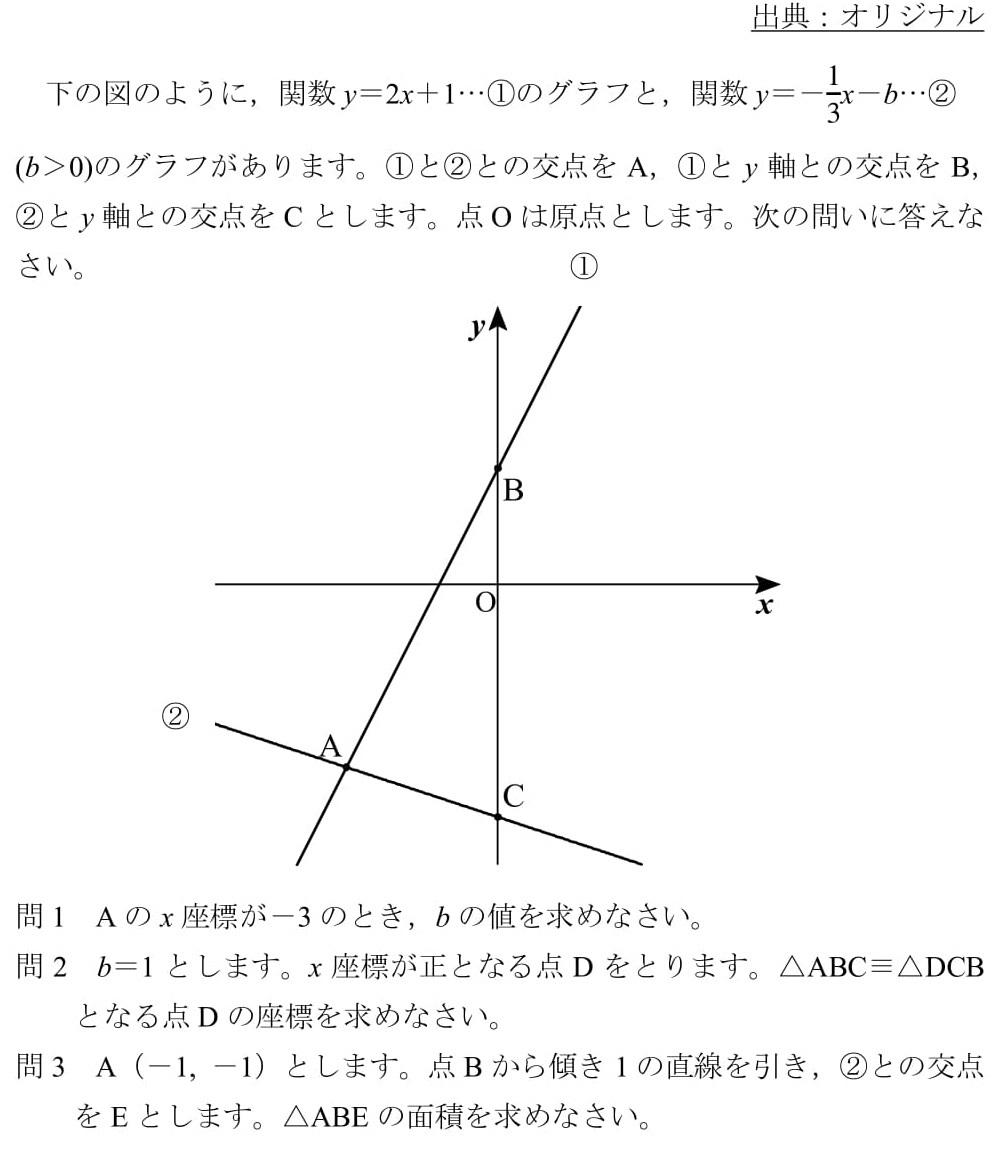 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 | 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
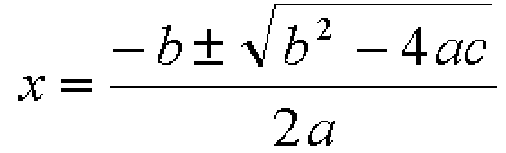 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 2次関数の接線の求め方を解説 |
2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 2次関数の接線の求め方を解説 |
2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 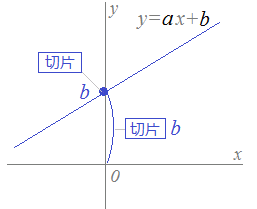 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 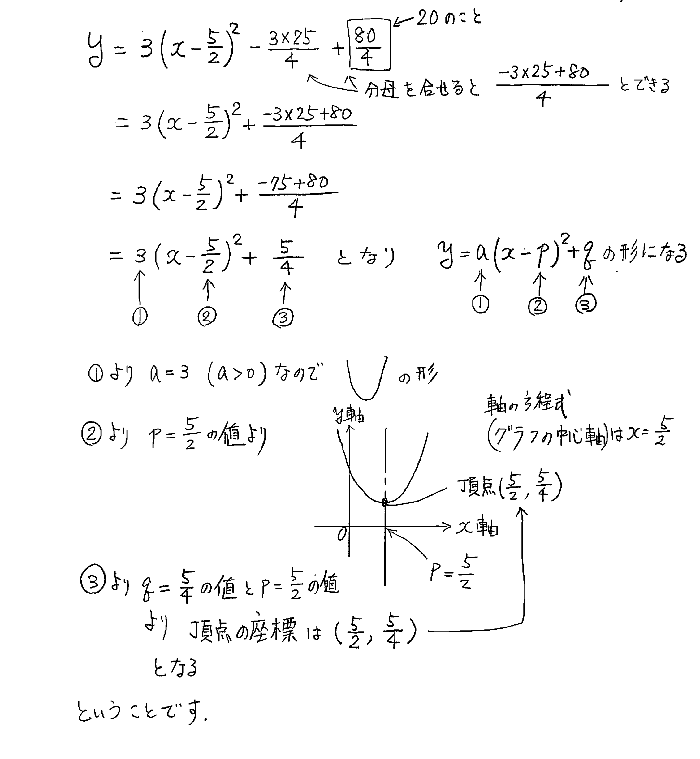 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 | 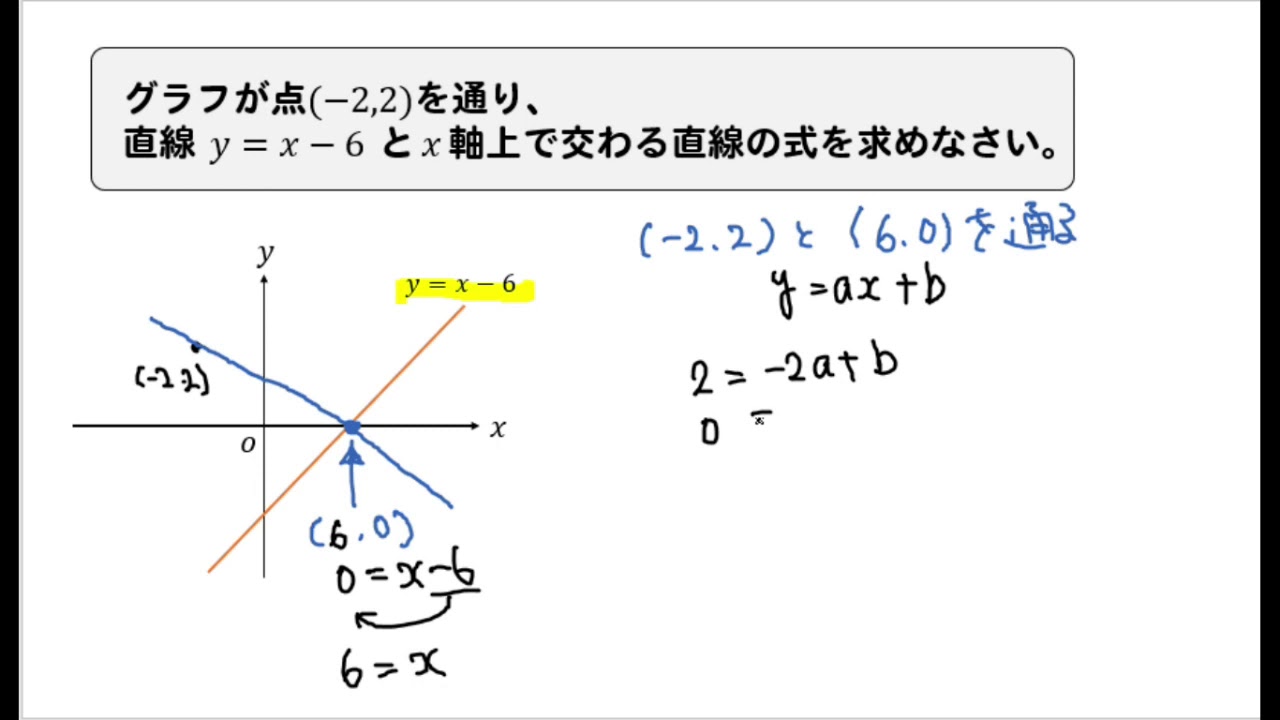 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 | 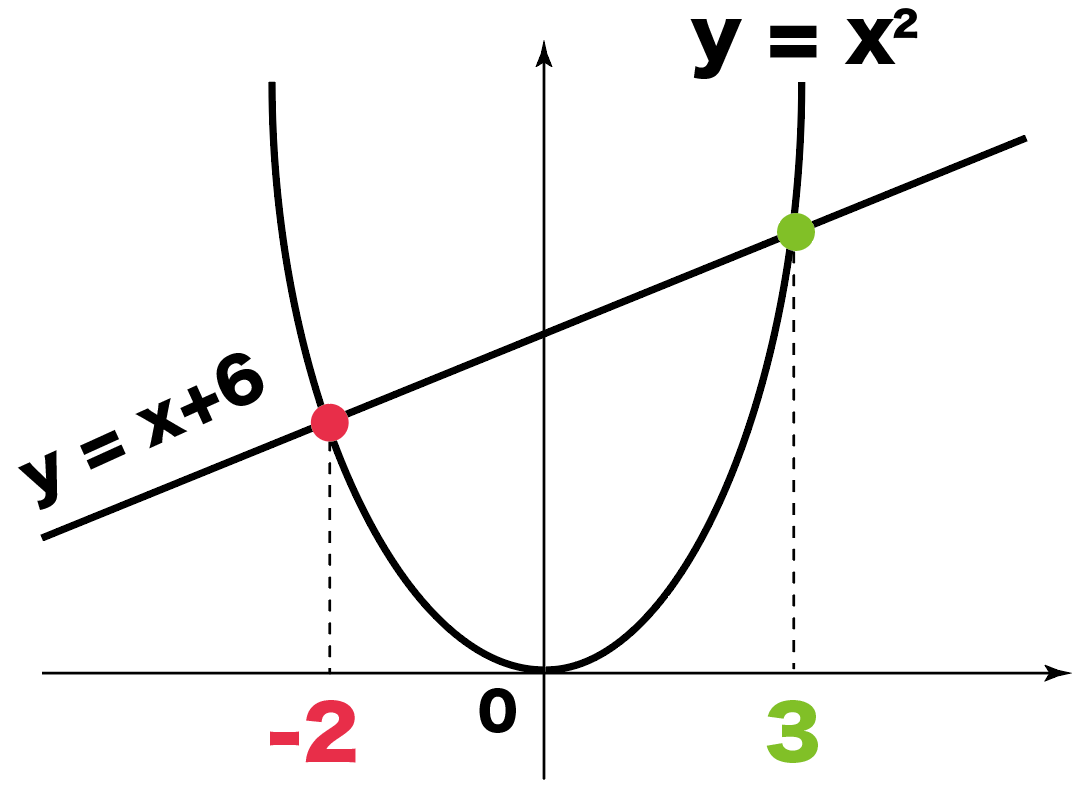 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 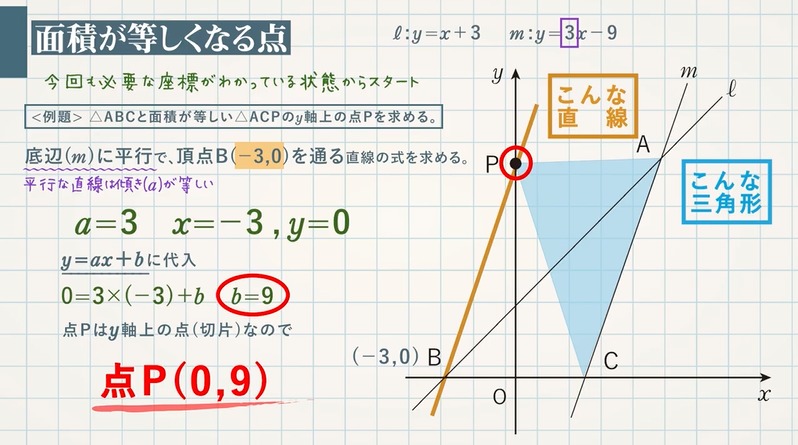 2次関数の接線の求め方を解説 |
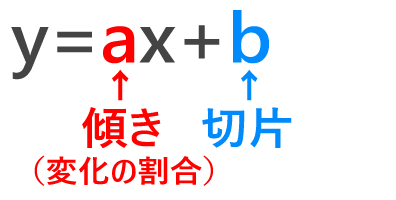2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |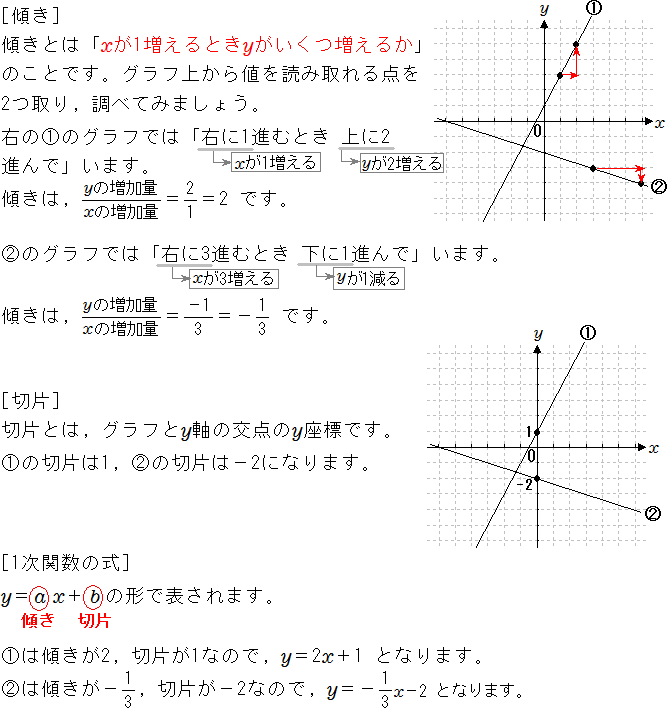
2次関数の接線の求め方を解説 | 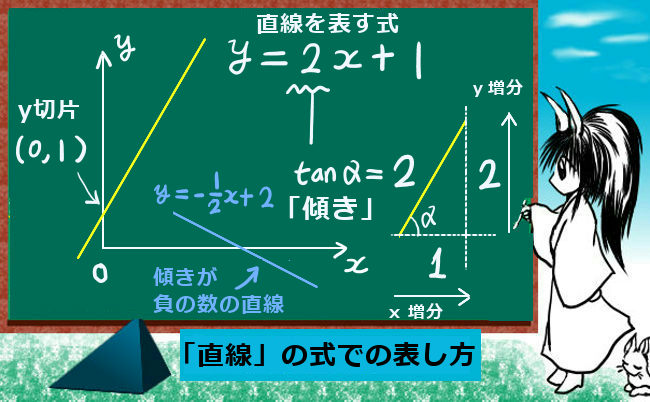 2次関数の接線の求め方を解説 |  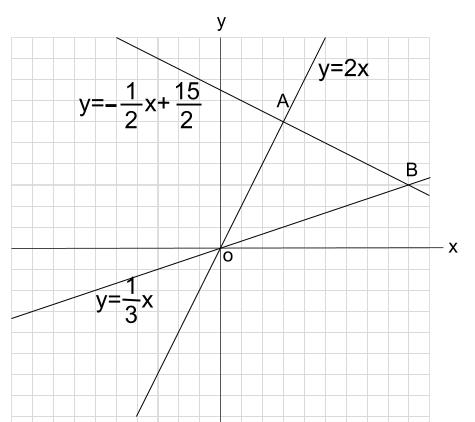2次関数の接線の求め方を解説 |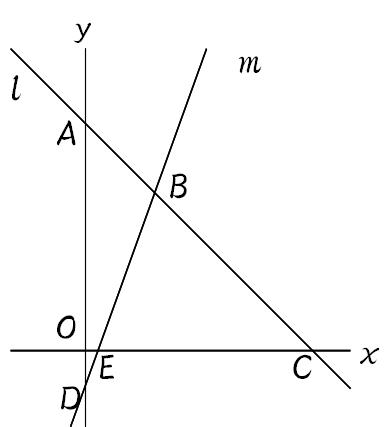
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |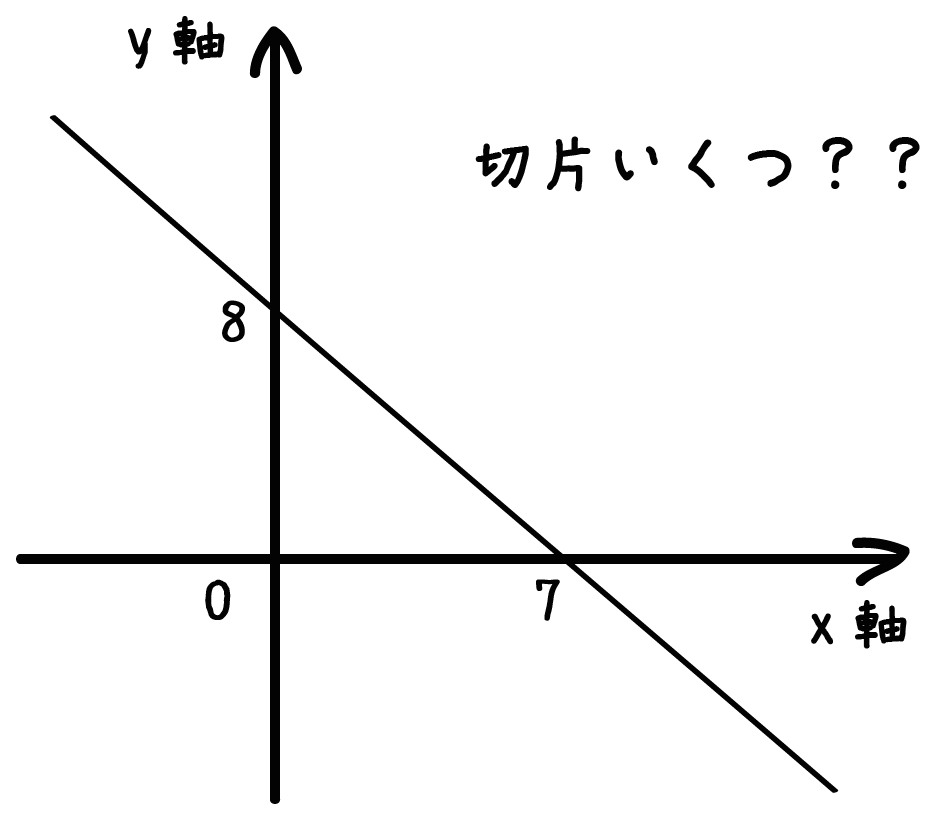
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 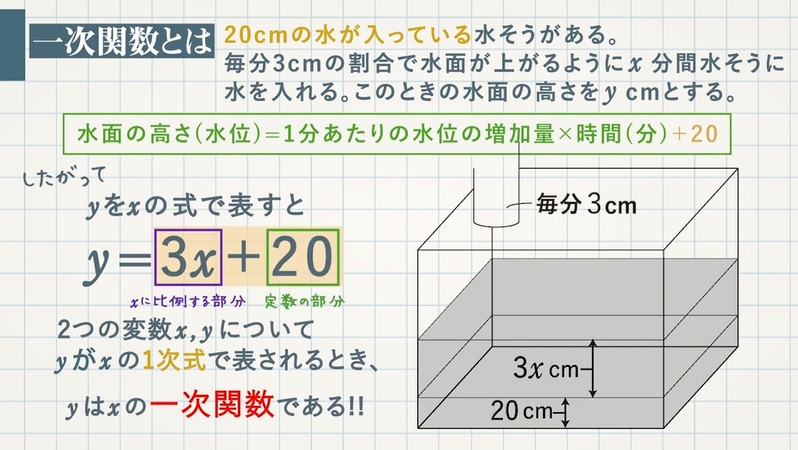 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 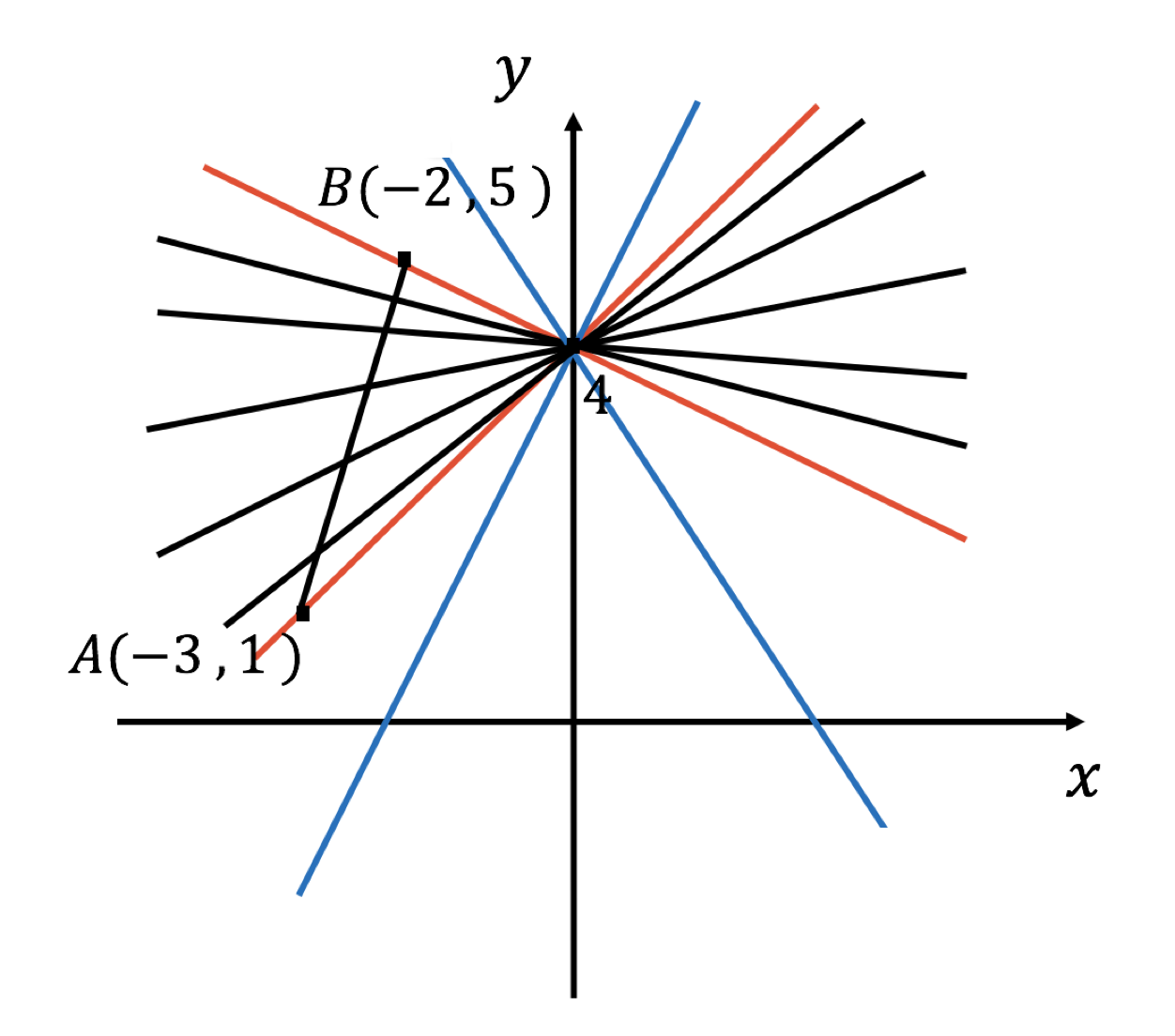 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 | 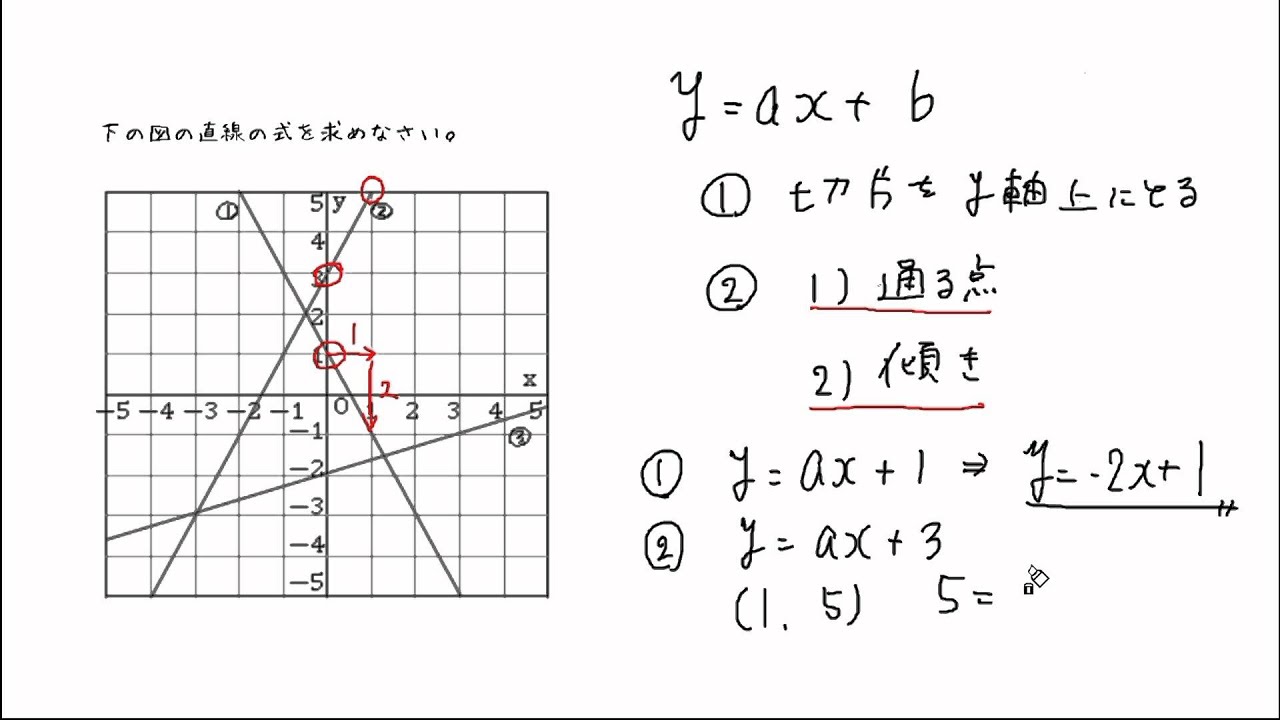 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 | 2次関数の接線の求め方を解説 | 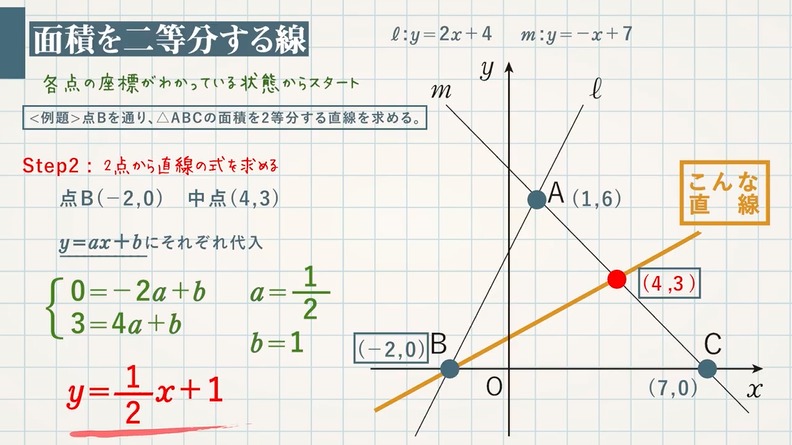 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 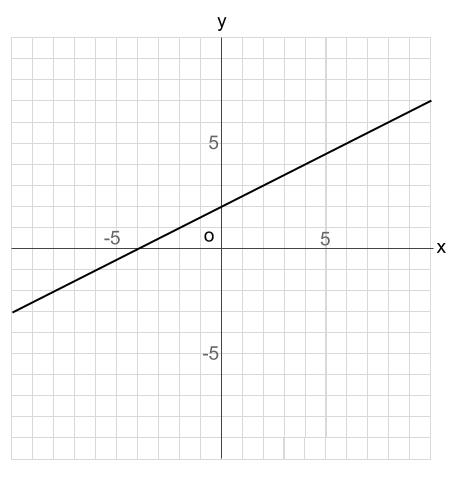 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 | 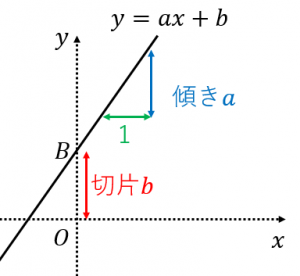 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 | 2次関数の接線の求め方を解説 |
 2次関数の接線の求め方を解説 |  2次関数の接線の求め方を解説 |
つまり、点線部が今求めたい関数です。 点 は 上にあるので、 (1) が成り立ちます。 また、点 と には次の関係が成り立ちます。 これを変形すると、 (2) となります。 (2)を(1)に代入 1/6 (βα)^3 の積分の公式の使い所 1/6公式は下図のように、2次以下の2つの関数によって囲まれた部分の面積を求めるような場合に使うことができます。
Incoming Term: 1次関数 公式, 1次関数 公式 2点, 1次関数 公式 中学, 1次関数 切片 公式, 1次関数 変化の割合 公式, 1次関数 傾き 公式, 1次関数 2点を通る 公式, 数学 1次関数 公式,
0 件のコメント:
コメントを投稿